-dB의 의미
콘솔의 페이더를 보면 0dB가 상단에 있고 그 밑으로 –로 표기되는 dB값들이 보입니다. -로 표기되는 dB값은 무엇일까? 의문을 가지고 계신 분들이 있을 겁니다. 0dB가 있는 데 과연 –로 표기되는 dB 값들은 무엇을 의미하는 걸까요?

전력이란 무엇인가?
일정 시간 동안 전류가 할 수 있는 일의 양을 말합니다. 단위는 W(와트)로 표기합니다. 전력, 전류, 전압의 관계를 공식으로 나타내면 다음과 같습니다.
P=E*I
(P:전력, E:전압, I:전류)
입니다.
전류와 전압, 저항의 관계를 나타내는 공식은
I=E/R, E=I*R
(R:저항)
입니다.
P=E*I에 대입하면
P=E*E/R
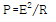
입니다.
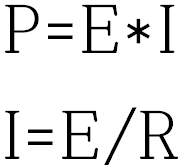
전압과 저항값을 알면 전력을 도출할 수 있습니다.
전압이 5V이고 저항이 50Ω일 경우 전력은
P=52/50=1/2=0.5W
입니다.
전압이 10V이고 저항이 여전히 50Ω일 경우 전력은
P=102/50=100/50=2W
입니다.
데시벨(dB) 개념 잡기

데시벨은 보통 음량을 나타낼 때 쓰는 단위입니다. 데시(Deci)와 벨(Bell)의 합성어입니다. 데시는 1/10을 의미하는 접두어이고 벨은 전화기의 발명가 알렉산더 그레이엄 벨의 이름에서 따온 것입니다. 두 개의 양에 대한 비율 즉 상대값입니다. 0dB를 기준으로 한 음량의 상대값, 전력과 전압의 상대값으로 계산한 결과치로 나타냅니다. 그리고 또 한가지의 특성이 있습니다. 데시벨은 대수(logarithm, 로그)입니다. 로그는 어떤 수를 나타낼 때 고정된 밑을 몇 번 곱하여야 하는가 하는 함수로써 표현합니다. 어떤 수를 몇 번 제곱해야 하는지로 표현하기 때문에 큰 수 또는 작은 수를 간단하게 치환하여 표현할 때 효과적입니다.
dB값 계산하기 1(전력으로부터)

이제 dB를 전력과 전압으로부터 계산해 보겠습니다.
원래 벨 값은 다음과 같이 구합니다.
Bell= log(P1/P0)
입니다. 이럴 경우 값이 너무 작아 10을 곱하여
dB=10log(P1/P0)
로 만들어 데시벨 값을 도출합니다.
위의 식에 나오는 P를 전력으로 상정하여 계산해 보겠습니다.
100W와 200W의 상대값으로 데시벨을 만들어 보겠습니다.
dB=10log200W/100W=10log2=10*0.301=3
입니다.
100W와 200W 즉 전력의 두 배 값은 3dB가 됩니다.
절대값의 차이는 상관이 없고 비율로 데시벨 값이 도출됩니다.
1W와 2W의 비율, 10W와 20W의 비율은 모두 3dB로 계산됩니다.
그러면 100W와 1,000W 사이의 비율은 몇 dB로 표시될까요?
dB=10log1,000W/100W=10log10=10*1=10
이 됩니다. 전력의 10배 차이는 10dB로 계산됩니다.
100W와 100,000W의 상대값을 dB로 환산하면 어떻게 될까요?
dB=10log100,000W/100W=10log1,000=10*3=30
30dB가 됩니다. 이것은 다음과 같이 계산할 수도 있습니다.
10dB의 10배, 100dB의 다시 10배 하였으므로
10+10+10=30dB가 됩니다.
이것을 달리 표현하면
100W와 100,000W의 상대값은 30dB입니다.
dB값 계산하기 2(전압으로부터)

먼저 알고 있어야 할 공식이 있습니다.
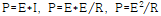
(P=전력, E=전압, R=저항)
이것을 데시벨을 계산하는 식에 대입해 보겠습니다.
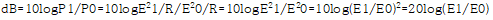
조금 복잡하게 되었습니다.
4V와 그 두 배인 8V를 공식에 대입해 보겠습니다.
dB=20log(8/4)=6dB가 됩니다.
전력의 두 배 상승으로 인한 dB값의 증가와 전압의 두 배 상승으로 인한 dB값의 증가는 연결되어 있습니다.
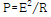
를 보면 전력은 전압의 제곱에 비례합니다.
전압을 두 배 올리면 전력을 4배 올릴 때 dB 변동값이 같고
전압을 10 배 올리면 전력을 100 올릴 때 dB 변동값이 같습니다.
예를 들어 보겠습니다.
전압은 10V=>20V
전력은 10W=>40W
일 때를 비교해 보겠습니다.
dB=20log20/10=6dB(전압을 2 배 올릴 때 6dB의 차이가 있습니다.)
dB=10log40/10=6dB(전력을 4 배 올릴 때 6dB의 차이가 있습니다.)
-로 표기되는 dB값
-dB값은 왜 생기는 걸까요? 이것은 0dB를 1W라는 기준값으로 정하기 때문입니다. 1W 밑으로 내려가는 0.***값을 로그 계산식에 넣으면 –값으로 나오기 때문입니다.
예를 들어 전력값이 0.5를 적용해 보겠습니다.
10log0.5=-3dB
가 됩니다.
1은 0.5의 두 배이기 때문에 -방향으로 3dB의 차이가 있습니다.
음향에 관련된 책들을 보면 전력과 dB값을 비교하여 표로 정리한 경우를 많이 보실 것입니다.
전력(Watt) / dB라고 했을 때
0.25 / -6, 0.5/-3, 1(기준)/0(기준), 2/3, 4/6, 8/9, 10/10, 100/20
식으로 정리되어 있을 겁니다.
이것은 dB와 전력을 측정하여 정리한 것이 아니고 공식을 적용한 계산식에서 도출한 값들입니다.
'음향' 카테고리의 다른 글
| VU미터(volume unit meter)와 피크미터(PPM:peak program meter) (0) | 2021.10.11 |
|---|---|
| dBm, dBu, dBV, dBW (0) | 2021.09.25 |
| 옴의 법칙(Ohm’s law)-저항, 임피던스, 리액턴시 (0) | 2021.09.10 |
| 교류에서 전압을 표시하는 방법-peak, peak to peak, Vav, RMS (0) | 2021.09.03 |
| 전기의 종류-직류와 교류 (0) | 2021.08.27 |




